迁移目标攻击文献阅读

Towards transferable targeted attack（2020CVPR）

代码链接：https://github.com/TiJoy/Towards-Transferable-Targeted-Attack

摘要

目标攻击比非目标攻击更难迁移，在本文中分析了两点造成这种困难的原因，1）在迭代攻击中存在梯度消失的现象，在累计动量时，相邻两次成功的噪声过分一致，造成噪声固化；2）目标对抗样本只与目标类别接近还不够，还要远离原始的类别。为解决上述问题引入庞加莱距离（Poincaré distance），作为相似性度量，使得在迭代攻击中梯度大小自适应以缓解噪声固化。进一步，在用度量学习（metric learning）对目标攻击过程正则化处理，使对抗样本远离真实标签并且获得高迁移目标对抗样本。lmageNet上的实验证实了我们的方法的优越性，在黑盒针对性攻击中，与其他最新技术相比,其攻击成功率平均提高了8%

庞加莱距离度量（Poincar´e Distance Metric）

大多数黑盒攻击使用softmax作为损失函数， \[ \frac{\partial L}{\partial o_{i}}=p_{i}-y_{i} \] $p_i$是预测概率，$y_i$是标签one-hot编码，对于目标攻击，损失函数对softmax输出的向量$o$，在迭代攻击中$p_i$逐渐靠近$y_i$，梯度消失，造成噪声固化，用Poincaré distance替代交叉熵损失可以解决这个问题。

关于Poincaré distance：

Poincaré ball上所有点都在一个单位n维$l_2$球上，两点间的距离定义如下： \[ d(u, v)=\operatorname{arccosh}(1+\delta(u, v)) \] 其中$u$和$v$是n维欧几里得空间$l_2$范数小于1的两点，$\delta(u,v)$是等距不变量定义如下 \[ \delta(u, v)=2 \frac{\|u-v\|^{2}}{\left(1-\|u\|^{2}\right)\left(1-\|v\|^{2}\right)} \]

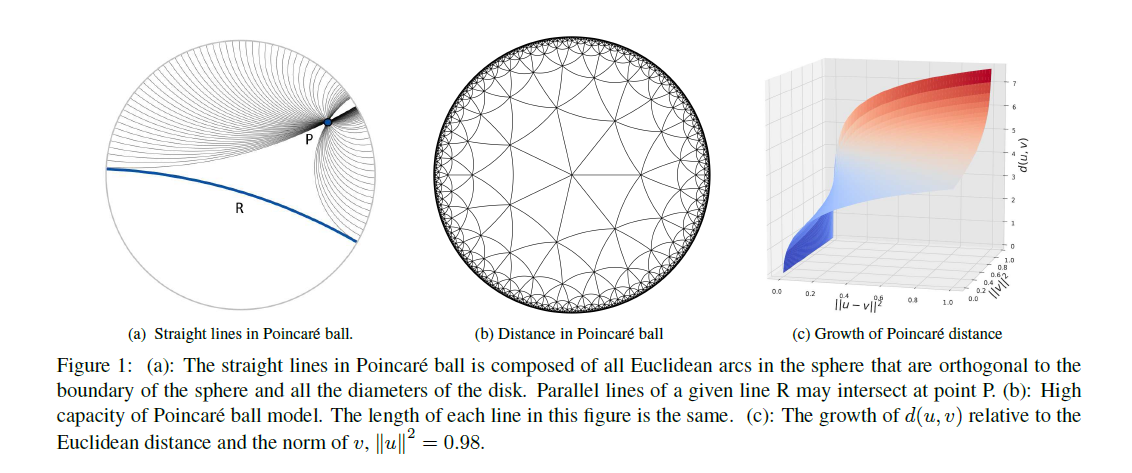
图b中任一点到边缘的距离都是$\infty$，图c中，当接近球的表面时，Poincaré distance增长非常快。这意味着当向表面移动时，梯度大小将会增长。

由以上定义，对于one-hot编码的标签$y$，有$\sum_{i}y_i=1$，这表示标签在一个单位$l_1$球上。当$y$是一个未经平滑处理的one-hot标签，有$\|y\|_2=1$，所以点$y$在Poincaré ball的边缘，这意味着任一点到$y$的距离都是$+\infty$ 。在目标攻击中，我们的目标是减少模型输出的logits和目标标签之间的距离。

但使用Poincaré distance存在另外一个问题，融合的logits不满足$\|l(x)\|_2<1$，所以本文中logits用$l_1$距离归一化。对于目标标签，任一点到它的距离是+$\infty$ ，这难以优化。将y减去一个非常小的常数$\xi=0.0001$ ，Poincaré distance 度量损失 \[ \mathcal{L}_{P o}(x, y)=d(u, v)=\operatorname{arccosh}(1+\delta(u, v)) \] 其中$u=l_k(x)/\|l_k(x)\|_1$，$v=\max \{y-\xi, 0\}$，$l(x)$是融合的logits。在本文中，$l(x)$是融合了多个模型的logits。 \[ l(x)=\sum_{k=1}^{K} w_{k} l_{k}(x) \] $K$是集成模型数量，$l_k(x)$表示第$k$个模型输出的logits，$w_k$是每个模型的权重，$w_k>0$($\sum_{k=1}^{K}w_k=1$) ，在本文中每个模型的权重相等。通过引入Poincaré度量，当且仅当数据接近目标标签时梯度才会变大。

目标攻击三元损失（Triplet Loss for Targeted Attack）

以往的目标攻击生成的对抗样本和原始类别过于接近，这不利于样本的迁移，本文中引入三元损失，三元损失不仅减少对抗样本和目标类别的距离，还增加对抗样本和原始标签的距离，本文使用干净样本的logits $l(x_{clean})$，one-hot编码的目标标签$y_{tar}$和真实标签$y_{true}$构成三元损失： \[ \begin{aligned} & \mathcal{L}_{\text {trip }}\left(y_{\text {tar }}, l\left(x_{i}\right), y_{\text {true }}\right) \\=& {\left[D\left(l\left(x_{i}\right), y_{\text {tar }}\right)-D\left(l\left(x_{i}\right), y_{\text {true }}\right)+\gamma\right]_{+} . }\end{aligned} \] 注意到$l(x_{adv})$没有归一化，本文中使用角距离（angular distance）作为距离度量： \[ D\left(l\left(x^{a d v}\right), y_{\text {tar }}\right)=1-\frac{\left|l\left(x^{a d v}\right) \cdot y_{\text {tar }}\right|}{\left\|l\left(x^{a d v}\right)\right\|_{2}\left\|y_{\text {tar }}\right\|_{2}} . \] 将三元损失加到损失函数，得到整个的损失函数： \[ \mathcal{L}_{\text {all }}=\mathcal{L}_{P o}\left(l(x), y_{\text {tar }}\right)+\lambda \cdot \mathcal{L}_{\text {trip }}\left(y_{\text {tar }}, l\left(x_{i}\right), y_{\text {true }}\right) \] 基于MI-FGSM，本文也使用输入多样性的方法，整体算法流程如下图：

实验

实验细节自己看

参考

https://blog.csdn.net/sydukee/article/details/110822003

https://www.jianshu.com/p/afaf551d145e

On Generating Transferable Targeted Perturbations（ICCV2021）

代码链接：https://github.com/Muzammal-Naseer/TTP

本文提出一种基于生成方法的高迁移目标扰动（transferable targeted perturbations，TTP)，现有的方法依赖于从一个模型到另一个模型的类别边界信息，不利于扰动的迁移。本文的方法匹配扰动图像的"分布"和目标类别，最后提出一种新的目标函数不仅对齐原始图像和目标图像的全局分布，也匹配两种域的局部邻域结构。基于所提出的目标，我们训练一个生成器，可以自适应地合成特定于给定输入的扰动。我们的生成方法与源或目标域标签无关，同时对广泛的攻击设定，始终比最先进的方法表现更好。

主要方法概括：提出一种新的生成训练框架，通过最大化源分布和目标分布在一个预训练的判别器隐空间共同一致性，将源分布映射为目标分布。

主要贡献

生成目标迁移：我们提出了一种新的生成方法来学习可迁移的目标对抗扰动。我们独特的训练机制允许生成器在训练期间探索增强的对抗性空间，这提高了推理期间对抗性样本的可转移性。
互相分布匹配：我们的训练方法是基于给定的源分布和目标分布之间的相互一致。因此，我们的方法可以对训练不需要分类边界信息的生成器提供有针对性的指导。这允许攻击者从无监督的特征中学习有针对性的生成扰动，并消除标记数据的成本。
邻域相似性匹配：除了全局分布匹配方面，我们在对抗和目标类样本之间引入批处理邻域相似性匹配目标，以最大化两个分布之间的局部对齐。

基于生成的目标攻击

生成模型

目标类别$t$，$P$和$Q$分别表示源域和目标域对抗样本，$x_s$ ~ $P$，$x_t$ ~ $Q$，扰动的源域数据$P^{\prime}$，$x^{\prime}$ ~ $P^{'}$，$x^{'}=x_s+\delta$，$\mathcal{D}_\psi(x_s)$，$\mathcal{D}_\psi(x^{\prime}_s)$，$\mathcal{D}_\psi(x_t)$分别代表潜在分布。

实验框架如下图，$\mathcal{G}_\theta$是生成器，$\mathcal{D}_\theta$是判别器，$\mathcal{G}_{\theta}$学习源域到目标域的映射，使源域图像获得最小改动，对抗扰动$\delta$限制在范数距离$l_{\infty} \leq \epsilon$，这通过一个可微的裁剪操作将无界的生成器$\mathcal{G}_\theta$生成的对抗扰动投影到距$x_s$固定范数距离内实现。 \[ x^{'}_s=clip(min(x_s+\epsilon,max(\mathcal{W}*\mathcal{G}_\theta,x_s-\epsilon))),\tag 1 \] $\mathcal{W}$是固定权重的平滑操作，在不破坏$l_{\infty}$范数限制下减少高频信息，使生成器收敛到一个有意义的结果。

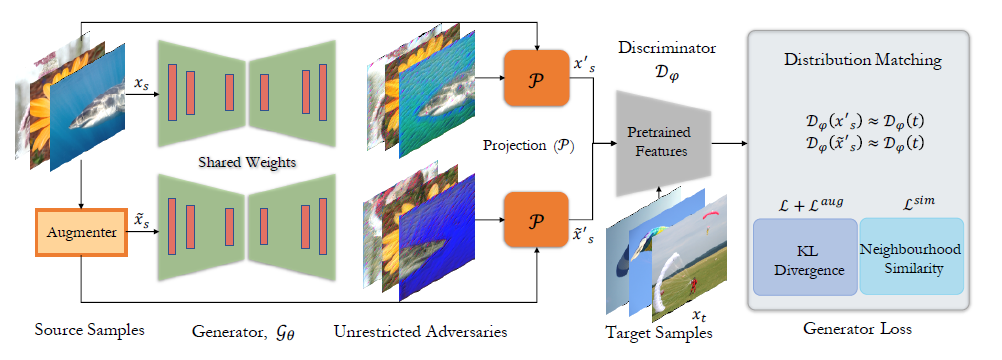
原有的基于生成的方法依赖于判别器的分类边界，攻击者必须可以获得一个大量标签数据训练的判别器，进一步生成器依赖于输入的特定实例特征，缺少对全局目标分布特征的把握，造成低迁移性。

为解决上述问题，本文对目标分布$Q$建模并使在隐层空间$\mathcal{D}_{\psi}$中扰动的源域分布$P^{'}$更接近于$Q$ \[ \left\| \delta \right\|_{\infty} \le \epsilon, s.t., \quad \mathcal{D}_\psi(x^{'}_s)\approx \mathcal{D}_\psi(x_t) \tag 2 \] 这个全局的目标函数有两个优势，1）减少扰动和目标分布的不匹配程度，为生成器提供一种引导，2）不需要目标类别信息，判别器可以是一种无监督的方式训练得到

分布匹配

用KL散度表示$p^{'}$和$Q$之间的共同一致性，判别特征$\mathcal{D}_\psi(x^{'}_s)$和$\mathcal{D}_\psi(x_t)$的KL散度定义如下 \[ D_{K L}\left(P^{\prime} \| Q\right)=\frac{1}{N} \sum_{i=1}^{N} \sum_{j=1}^{n} \sigma\left(\mathcal{D}_{\psi}\left(\boldsymbol{x}_{s}^{\prime, i}\right)\right)_{j} \log \frac{\sigma\left(\mathcal{D}_{\psi}\left(\boldsymbol{x}_{s}^{\prime, i}\right)\right)_{j}}{\sigma\left(\mathcal{D}_{\psi}\left(\boldsymbol{x}_{t}^{i}\right)\right)_{j}} \] N代表样本数量，n是判别器输出的特征维数，$\sigma$表示sigmoid操作，由于KL散度非对称$D_{K L}\left( P^{\prime} \| Q\right)\neq D_{K L}\left(Q \| P^{\prime}\right)$，不是一种距离的度量，损失函数定义 \[ \mathcal{L}=D_{K L}\left(P^{\prime} \| Q\right)+D_{K L}\left(Q \| P^{\prime}\right)\tag{3} \] 作为一种常规性度量，引入在分布对齐时添加源域样本的增广版本，这能使生成器更关注于特定目标类类别信息，对输入变换更鲁棒。本文中随机使用旋转，裁剪，水平翻转，颜色抖动或者灰度处理变换，从源域$x_s$得到增广样本$\widetilde{x}_s$ 。$\widetilde{x}_s$ ~ $\widetilde{P}$送入生成器$\mathcal{G}_{\theta}$ ，扰动的增广样本$\widetilde{x}_s ^{'}$ ~ $\widetilde{P}^{'}$ 用公式（1）投影到增广样本附近，目标域样本没有任何增广操作，$\widetilde{x}_s ^{'}$ 送入判别器计算$ _(^{}s)$和$ (x_t)$之间的共同一致性，公式如下 \[ \mathcal{L}^{a u g}=D_{K L}\left(\tilde{P}^{\prime} \| Q\right)+D_{K L}\left(Q \| \tilde{P}^{\prime}\right) \tag 4 \]

邻域相似度匹配

上述损失函数没有考虑局部结构，例如一个样本和它增广版本之间的关系，为了扰动的源域和目标类别样本的可靠对齐，提出匹配两种域之间的邻域相似度分布。考虑一批目标域样本$\left\{x_{t}^{i}\right\}_{i=1}^{N}$和一批扰动的源域样本$\left\{x_{s}^{'i}\right\}_{i=1}^{N}$ ，对于一个训练批次$x_s ^{'}$，计算相似度矩阵$\mathcal{S}^s$，它的元素编码了原始样本和它的增广版本$\widetilde{x}_s ^ {'}$之间的余弦相似度。 \[ \mathcal{S}_{i, j}^{s}=\frac{\mathcal{D}_{\psi}\left(\boldsymbol{x}_{s}^{\prime, i}\right) \cdot \mathcal{D}_{\psi}\left(\tilde{x}_{s}^{\prime, j}\right)}{\left\|\mathcal{D}_{\psi}\left(x_{s}^{\prime, i}\right)\right\|\left\|\mathcal{D}_{\psi}\left(\tilde{x}_{s}^{\prime, j}\right)\right\|} \tag 5 \] 作为对比，对于目标类别样本$x_t$ ，计算样本之间的余弦相似度矩阵$\mathcal{S}^t$ \[ \mathcal{S}_{i, j}^{t}=\frac{\mathcal{D}_{\psi}\left(x_{t}^{i}\right) \cdot \mathcal{D}_{\psi}\left(x_{t}^{j}\right)}{\left\|\mathcal{D}_{\psi}\left(x_{t}^{i}\right)\right\|\left\|\mathcal{D}_{\psi}\left(x_{t}^{j}\right)\right\|} \tag6 \] 对上面两个相似度矩阵沿着每一行做softmax操作得到概率估计 \[ \overline{\mathcal{S}}_{i, j}=\frac{\exp \left(\mathcal{S}_{i, j}\right)}{\sum_{k} \exp \left(\mathcal{S}_{i, k}\right)}, where, \mathcal{S} \in\left\{\mathcal{S}^{s}, \mathcal{S}^{t}\right\} \tag 7 \] 为了匹配源域和目标域局部邻域模式，计算$\overline{\mathcal{S}}^s$和$\overline{\mathcal{S}}^t$KL散度作为损失项 \[ \mathcal{L}^{s i m}=\sum_{i, j} \overline{\mathcal{S}}_{i, j}^{t} \log \frac{\overline{\mathcal{S}}_{i, j}^{t}}{\overline{\mathcal{S}}_{i, j}^{s}}+\sum_{i, j} \overline{\mathcal{S}}_{i, j}^{s} \log \frac{\overline{\mathcal{S}}_{i, j}^{s}}{\overline{\mathcal{S}}_{i, j}^{t}} \tag 8 \]

整体损失函数

生成器参数通过最小化下面损失更新 \[ \mathcal{L}_{\mathcal{G}}=\mathcal{L}+\mathcal{L}^{a u g}+\mathcal{L}^{sim } \tag 9 \] 上述损失激励生成器在扰动源域样本时不仅匹配目标分布的全局特征（$\mathcal{L}+\mathcal{L}^{a u g}$），而且基于邻域连通匹配局部信息（$\mathcal{L}^{sim }$）

整体算法流程

实验

实验细节自己看吧，对比了很多基于迭代和基于生成的模型

On Success and Simplicity: A Second Look at Transferable Targeted Attacks（NeurIPS 2021）

代码链接：https://github.com/ZhengyuZhao/Targeted-Tansfer

本文提出一个简单的logit损失，相比于资源密集型的模型取得了更好的目标迁移效果，在三个新的现实场景：

低模型相似度的集成迁移（ensemble transfer）
a worse-case scenario with low-ranked target classes
Google Cloud Vision API 真实世界的攻击

中验证了所提方法的优越性，并展示了这个损失对data-free方法生成的目标通用扰动的实用性。

简介

目前目标攻击 resource-intensive transferable attacks可以取得SOTA效果，主要有两种方法：FDA和TTP。FDA的方法[1][2]通过在大规模标签数据上训练target-class-specific辅助分类器，然后再深度特征空间中，用辅助分类器优化对抗扰动。TTP[3]方法基于匹配全局和局部分布训练target-class-specific 对抗生成网络（GANs）,然后使用训练好的生成器对任意输入图像直接生成扰动。

本文主要贡献在于发现不需要模型训练和外加数据的简单迁移攻击(MI-FGSM，DI-FGSM，TI-FGSM)也能实现强目标迁移性。我们认为这一观点被忽略了，主要是因为目前的研究只使用了少量的迭代次数不合理地限制了攻击收敛性，另一个主要贡献是阐述非常简单的logit loss的普遍优越性，甚至比 resource-intensive SOTA方法表现更好。

对简单迁移攻击的新见解

集成三种迁移攻击（MI, DI, TI）可以获得最好效果，其实只使用DI就已经能获得很好的迁移效果，MI和TI和原本效果不好的目标攻击效果差不多。DI比TI表现更好的原因可能是由于DI在每次迭代时随机图像增广而不是TI的固定增广。在这种方式下，对目标攻击的梯度更具有一般性，所以能避免对白盒源模型的过拟合。（？？？不理解）MI和DI，TI有本质区别，它只能固定更新方向，而不能用于向一个特定（目标）实现更准确的梯度方向。

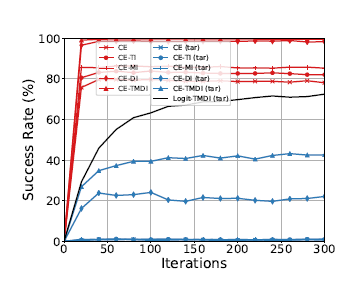
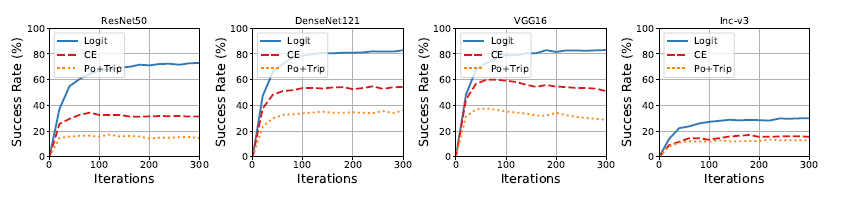
图1.

通常目标迁移攻击限制攻击将攻击优化限制在少数迭代（通常小于20次）。在图1中目标攻击比非目标攻击达到收敛所需要的迭代次数更多。这意味着在只有少数迭代的情况下评估目标迁移性是有问题的。

现有简单攻击通常使用交叉熵（CE）损失。但随着迭代次数增加，CE损失会造成梯度消失。为解决这个问题，Po+Trip 损失[4]以一种贪婪的方式随意的逆转梯度的减少，例如在迭代时增大梯度。然而我们发现这种操作导致迭代次数太大，因此造成攻击优化错过最小值。

在这里，对于损失函数，我们消除了CE损失中使用的最终softmax函数，只是从logit输出中反向传播梯度。 \[ L_{Logit }=-l_{t}\left(x^{\prime}\right) \tag 1 \] $l_t(·)$表示对目标类别 logit的输出。虽然用logit攻击的想法并不新，但它在目标迁移性方面的优越性能至今还没有被认识。我们还发现，使用著名的基于logit的损失，C&W，得到的结果一直比较糟糕。

下面公式$\eqref{eq22}$展示logit损失比CE损失有更强的梯度。CE损失对目标logit输入$z_t$的梯度对$p_t$单调递减，因为使用softmax函数，$p_t$很快到达1，因此梯度几乎消失。这种现象使得即使应用更多的迭代，也很难改善攻击。公式$\eqref{eq3}$logit损失是一个常数。 \[ \begin{aligned} L_{C E} &=-1 \cdot \log \left(p_{t}\right)=-\log \left(\frac{e^{z_{t}}}{\sum e^{z_{j}}}\right)=-z_{t}+\log \left(\sum e^{z_{j}}\right) \\ \frac{\partial L_{C E}}{\partial z_{t}} &=-1+\frac{\partial \log \left(\sum e^{z_{j}}\right)}{\partial e^{z_{t}}} \cdot \frac{\partial e^{z_{t}}}{\partial z_{t}}=-1+\frac{e^{z_{t}}}{\sum e^{z_{j}}}=-1+p_{t} \end{aligned} \tag 2\label {eq22} \]

\[ L_{\text {Logit }}=-z_{t}, \frac{\partial L_{\text {Logit }}}{\partial z_{t}}=-1 \tag 3 \label{eq3} \]

实验

实验数据集：NIPS 2017对抗攻击和防御数据集，在TI中$\|W\|_1=5$，所有攻击迭代次数300。

单个模型迁移效果

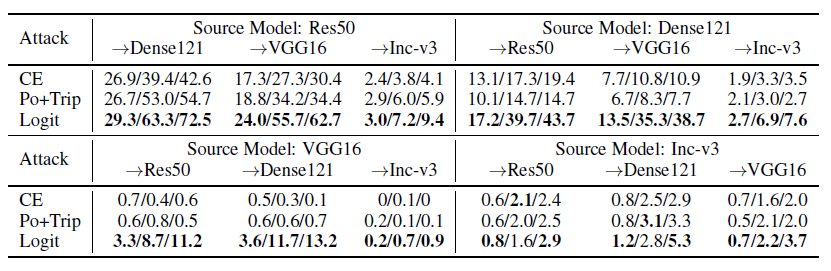
目标模型是resnet和densenet时目标迁移攻击成功率较高，一种解释是网络中的跳跃连接（skip connection）提高迁移率[5,6]，目标模型是Inception-v3 迁移成功率较低，一个可能的原因是Inception 结构有多尺度卷积和两个辅助分类器。

在简单和有挑战性场景下的集成迁移

（1）在简单情况下Po+Trip 在迭代次数限制在20次时效果比CE好，在足够迭代次数效果变差，下表对应20/100迭代次数。

（2）在源模型和目标模型没有交叉，logit方法攻击效果比CE和Po+Trip 有显著提升。三种方法比单个模型情况都有本质提升。Po+Trip方法在一些情况下表现最差因为它随机增加梯度大小，因为模型的多样性，损失面不光滑，造成优化过程错过最小值点。和单个模型的迁移场景一样，这种情况下Inception-v3的迁移也是最困难的。

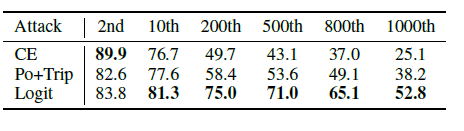
（3）目前基于迁移攻击的评估仅限于攻击最佳和平均的情况，为了解决这一局限性，我们考虑了一种更坏的转移情况，通过将目标从最高排序类别逐渐改变为最低排序的类别。在下表中，目标类别排名位置和目标迁移率有不可忽略的关系。具体地说，当目标标签预测概率越低，攻击越困难，排名较高的目标的结果可能不会像排名较低的目标的更现实、更糟糕的情况那样揭示不同攻击的实际强度。特别是，只看排名最高的目标的最佳情况可能会导致一个误导性的结论，即CE是最有效的攻击。这一发现表明，对目标可迁移性的更有意义的评估应进一步增加难度，超越目前的最佳和平均情况。

（4）对Google Cloud Vision迁移攻击。API预测了一组语义标签和置信度分数。具体来说，只返回顶部置信度不低于50%的类，最多显示10个类。请注意这里的置信度分数不是概率(总和为1)。我们测试了目标和非目标的可迁移性。由于所有返回的标签都具有较高的可信度($\ge$ 50%)，我们不会将成功率的衡量限制在top-1类别。相反，对于非目标成功率，我们测试真实标签是否出现在返回的列表中，而对于目标成功率，测试目标类是否出现。由于API预测的语义标签集并不完全对应1000个ImageNet类，所以我们将语义相似的类视为同一个类。

表4报告了超过100张图像的平均结果，这些图像最初产生的是正确的预测。可以看出，总的来说，实现目标转移的成功要比非目标转移的成功困难得多。特别是，Logit攻击实现了最佳的目标可迁移性，图4中显示了准不可察觉的扰动。我们的研究结果揭示了Google Cloud Vision在简单的基于迁移的攻击中存在的潜在漏洞，这种攻击不需要查询交互。

Logit方法和Resource-Intensive迁移攻击方法对比

（1）和TTP对比

参数：10-Targets（all-source），单个模型情况：ResNet50，集成模型情况ResNet{18,50,101,152}。目标模型：DenseNet121 和 VGG16 bn。

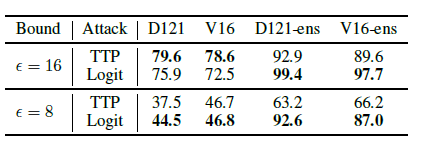
在上表中，在一般情况下$\epsilon=16$，logit攻击能获得和TTP差不多的效果，集成模型对logit攻击提升更大，这可能是因为即使使用单模型作为判别器，TTP也可以通过训练很好地学习目标语义的特征和通过大规模数据学习目标类别分布。图5. 通过比较TTP实现的无边界扰动与Logit实现的无界扰动，可以确定TTP学习到的更清晰的目标语义。

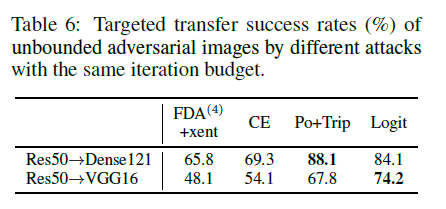
（2）和$\text{FDA}^{N}$+xent方法对比

CE, Po+Trip, 和 Logit三种方法和$\text{FDA}^{N}$+xent 在生成无边界对抗图像对比，对抗扰动初始化为随机高斯噪声并且要求越大越好。在4000张图像上实验，每一张图像朝着随机目标优化。MI迁移模型在无边界情况下有损表现，去除。表6所有的三种简单迁移攻击都比$\text{FDA}^{N}$+xent的方法要好，在图5中无边界的对抗扰动能够在某种程度上反应目标的语义。这一发现表明，实现目标可迁移性依赖于鲁棒的，语义特征，这些特征被各种模型所学习，也被人类所理解。这样，实现有目标的可迁移性与非有目标的可迁移性有本质区别，非目标攻击攻击非鲁棒特征就足够。同样值得注意的是，在具有较小范数边界的实际场景中，语义对齐扰动不改变人类的判断。

（3）简单Logit攻击在Data-Free通用扰动应用

上述对扰动的观察可以反映出特定的目标语义激励我们应用Logit攻击来实现目标的通用对抗扰动(UAPs)，这可以将多个原始图像分类到特定的目标类。现有的实现目标通用扰动主要依赖于对附加数据的大规模优化。然而，简单logit攻击能容易的扩展到data-free目标通用扰动，上述迁移logit攻击和唯一区别是用平均图像（所有像素值设为0.5而不是[0, 1]）作为原始图像。

在我们的实验中，对于每个目标类，我们进行300次迭代生成一个单一的目标UAP向量($\epsilon$ = 16)，并将其应用到我们数据集中的所有1000张图像。表7报告了所有1000个ImageNet类的平均结果。可以看出，logit loss可以带来实质性的成功，明显优于CE损失。图6可以确认这一点，图6显示了logit攻击可以产生比CE更多的语义对齐的扰动。这个观察结果也支持来自[7]的结论，即通用扰动包含域特征，而图像就扰动而言就像噪音。

结论和回顾

在这篇论文中，我们已经证明了实现有针对性的可迁移并不像目前的工作总结的那么困难。具体地说，我们发现，当给定足够的收敛迭代时，简单的可转移攻击实际上可以实现惊人的目标可迁移性。我们已经在广泛的场景中验证了简单可迁移攻击的有效性，包括三个新引入的具有挑战性的场景。这些具有挑战性的场景更好地揭示了不同攻击的实际能力。特别地，我们证明了一个非常简单的Logit攻击在所有迁移场景中都具有优越性，可以获得比最先进的资源密集型（resource-intensive）方法更好的结果。我们还展示了Logit攻击在以无数据方式产生目标通用对抗扰动方面的潜在应用。总的来说，我们希望我们的研究成果能够对未来的研究工作有所启发，对目标可迁移性进行更有意义的评估。我们未来的工作将集中于研究为什么不同的模型架构产生不同的可移植性。特别的我们应该去探索Inception-v3的低成功率。接下来，需要从多个方面对不同攻击的资源消耗进行更全面的讨论，例如训练和推理时间、硬件资源和数据大小。

较强的可移动性明显有利于对抗性图像在黑盒社交公益上应用。此外，考虑到我们的发现，即使是简单的攻击也可以产生高度可迁移的对抗图像，这也将激励社区设计更强大的防御。我们的方法仍有可能被恶意行为者滥用，以破坏合法的系统。然而，我们坚信，我们的论文能够为研究人员提供的帮助远远大于它可能为一个实际的恶意行动者提供的帮助。

参考文献

[1] Nathan Inkawhich, Kevin Liang, Lawrence Carin, and Yiran Chen. Transferable perturbations of deep feature distributions. In ICLR, 2020.

[2] Nathan Inkawhich, Kevin J Liang, Binghui Wang, Matthew Inkawhich, Lawrence Carin, and Yiran Chen. Perturbing across the feature hierarchy to improve standard and strict blackbox attack transferability. In NeurIPS, 2020.

[3] Muzammal Naseer, Salman Khan, Munawar Hayat, Fahad Shahbaz Khan, and Fatih Porikli. On generating transferable targeted perturbations. In ICCV, 2021.

[4] Maosen Li, Cheng Deng, Tengjiao Li, Junchi Yan, Xinbo Gao, and Heng Huang. Towards transferable targeted attack. In CVPR, 2020.

[5] Nathan Inkawhich, Kevin Liang, Lawrence Carin, and Yiran Chen. Transferable perturbations of deep feature distributions. In ICLR, 2020.

[6] Nathan Inkawhich, Kevin J Liang, Binghui Wang, Matthew Inkawhich, Lawrence Carin, and Yiran Chen. Perturbing across the feature hierarchy to improve standard and strict blackbox attack transferability. In NeurIPS, 2020.

[7] Chaoning Zhang, Philipp Benz, Tooba Imtiaz, and In So Kweon. Understanding adversarial examples from the mutual influence of images and perturbations. In CVPR, 2020.

Li's Blog