A Little Robustness Goes a LongWay: Leveraging Robust Features for Targeted Transfer Attacks(NIPS2021)
代码:尚未开源
提出的问题
之前的研究指出目标攻击很难迁移[1],之前对迁移对抗样本的研究主要集中在改进生成成功的图像扰动的优化方法,本文研究了用于构建对抗样本的源神经网络对样本迁移的影响。本文提出略微鲁棒的CNN—被训练成对小的对抗扰动具有鲁棒性的网络,可以被利用来大幅提高目标对抗样本对不同架构的可迁移性,针对一个稍微鲁棒的CNN构建的目标对抗样本可以迁移到 transformer。同时每个单独的略微鲁棒的神经网络都能有效地将特征转移到所有测试的非鲁棒网络,这表明略微鲁棒的网络依赖于与每个非鲁棒网络重叠的特征,尽管任何特定的非鲁棒网络的特征并没有与所有其他非鲁棒网络严重重叠。
此外,本文利用对抗迁移技术来检验哪些特征是由神经网络学习的。根据先前的工作[2],本文发现,在从非鲁棒(标准)到高鲁棒的分类器的频谱上,那些只有轻微鲁棒的分类器生成出最可能迁移的 representation-targeted 对抗样本,这表明轻微鲁棒的网络的特征与每个被测试的目标网络有很大的重叠。这可以解释为什么略微鲁棒的网络会产生更多可迁移对抗攻击,并且对于下游的迁移学习任务有更好的权重初始化。
主要贡献:
- 相对于标准(非鲁棒)网络产生的对抗样本,针对轻微鲁棒的CNN产生的对抗样本更容易迁移,这种迁移不仅扩展到其他CNN,也扩展到 transformer 结构。
- 随着源网络鲁棒性的增加,目标对抗样本对对抗防御网络的可迁移性也有大幅提高。
- 研究了对抗损失函数在产生可迁移的对抗样本中的作用。
- 非鲁棒的神经网络没有表现出实质性的特征(表征)可迁移性,而稍微鲁棒的神经网络则表现出可迁移性。这有助于解释为什么略微鲁棒的神经网络能使目标对抗样本的可迁移性更强。
实验
Transferability of Adversarial Examples
从 ImageNet validation 随机挑选1000张图片,每张图片类别不同,随机为每张图片挑选目标类,保证目标类和原始类别不同。用TMDI-FGSM 方法迭代300步生成对抗样本。实验用到的 CNN 模型有:Xception,VGG,ResNet,Inception,MobileNet,DenseNet,NASNetLarge,EfficientNet,transformer 模型有:ViT,LeViT,CCT,CLIP
Transferability to Convolutional Network Classifiers
针对具有小的鲁棒性参数的源网络进行优化的对抗样本,与非鲁棒性(\(\epsilon = 0\))网络的成功率相比(图1),在目标和非目标设定中都提高了迁移成功率。成功率的峰值对于每一个CNN目标网络大致相同(\(\epsilon = 0.1\))
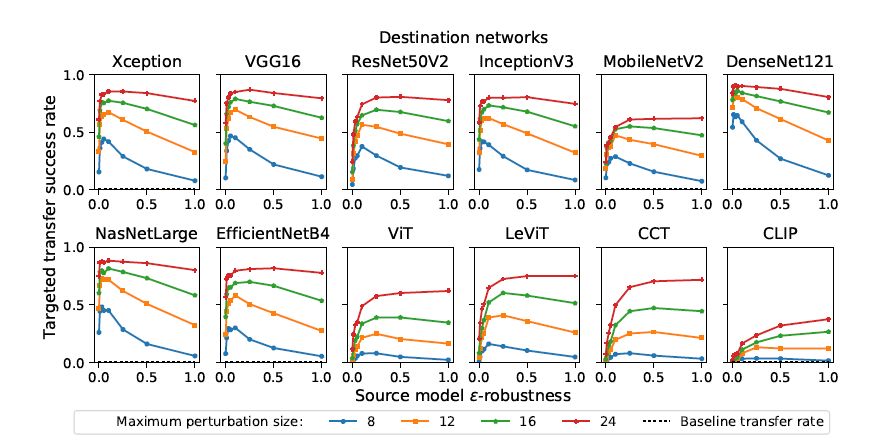
图 1:针对 ImageNet 分类器的目标迁移攻击成功率,使用相对于 "鲁棒的 ResNet50 源模型优化的对抗样本。成功率是指被目标网络分分类为目标类的对抗样本的比例。值越高攻击越成功。Baseline 是指未受干扰的图像被分类为目标类别的比率。(最好以彩色查看)。
当 \(\epsilon\) 超过最佳值,攻击成功率会快速下降,我们假设,当源网络的鲁棒性增加到一定程度后,网络开始完全忽略(非鲁棒性)目标网络所依赖的许多非鲁棒性特征,因此攻击不会修改这些特征,从而降低攻击的成功率。
Transformer-Based Classifiers
以前的研究中使用非鲁棒源网络的方法在使用卷积源模型构建目标的可迁移的对抗样本时几乎完全无效(表1)。这表明,基于 transformer 的模型和非鲁棒卷积模型所学习的特征在很大程度上是不同的。
使用略微鲁棒的 ResNet50 分类器作为源网络,可以极大地提高目标对抗样本对 transformer 分类器的迁移性。源网络的最佳鲁棒性参数对于目标 transformer 网络和目标卷积网络是不同的 ,尽管我们发现源模型中任何数量的鲁棒性(低于一个临界值)都会大大改善可迁移性。因此,在现实世界的黑箱攻击设置中—目标网络的架构是完全未知的—攻击者可以在源网络鲁棒性参数之间找到一个平衡点,使CNN分类器和基于 transformer 的分类器的迁移性能达到最佳。
表 1:\(l_{\infty}\)范数,扰动上限 16/255
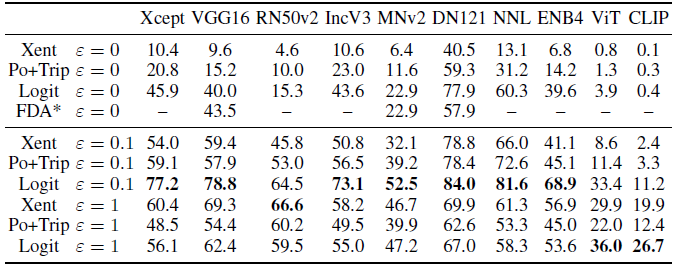
表1也比较了三种不同损失下的目标攻击攻击成功率。
对经过对抗训练的模型的攻击。用于攻击模型的对抗扰动大小设置的要比对抗训练让模型鲁棒的扰动数值要大,没有鲁棒性的模型作为源模型时对抗样本迁移失败,源模型的鲁棒性越高,攻击成功率也越高。
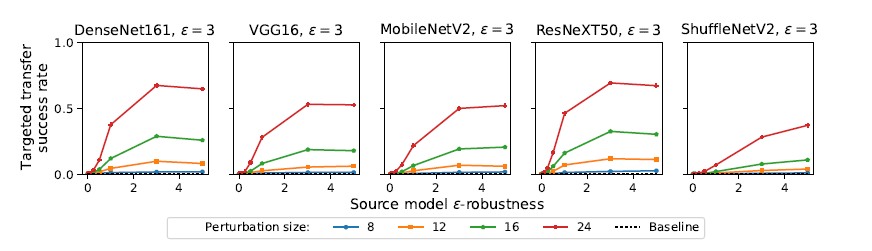
图 2:对对抗训练的鲁棒模型的攻击(\(\epsilon = 3\)),源模型是\(\epsilon\) - robust ResNet50
Adversarial Transferability of Features 特征的对抗迁移
这一部分展示略微鲁棒的网络比非鲁棒的网络和更鲁棒的网络表现出更高程度的表征可迁移性。这可以直接解释为什么用略微鲁棒的源网络构建的目标类对抗样本更容易转移,因为用略微鲁棒的网络生成的对抗样本将大量地转移特征,因此将较少地依赖少数可能不存在于每个模型中的高度脆弱的特征。
实验设计出发点:\(x\) 和 \(y\) 是两个在源模型特征表达层(倒数第二层)非常相似的两个样本,如果源模型对目标模型的特征迁移程度很高,那么 \(x\) 和 \(y\) 在目标模型的特征表达应该也非常相似。
从 ImageNet 测试集随机选择10张图像作为目标\(x\),选择990张图像作为初始图像\(y_0\),这1000张图像类别互不相同,对于每一个源模型,每一个目标类别,用 \(y0\) 构造对抗样本,攻击算法和上一部分同为 TMDI-FGSM。对于每一个类别,990个 representation-targeted 的对抗样本 \(y\) 应该和 \(x\) 在源模型有相似的特征表达,通过度量(\(x\),\(y\))在目标模型的表达,可以度量源模型的特征迁移能力。
采用两种度量相似性的方法,一种直观的方法是用 t-SNE 画出每一个 representation-targeted 对抗样本 \(y\) 在目标模型的特征表达向量(图 3)。每一种颜色代表一个类别,每一张图中的⭐代表每一个目标 t-SNE 嵌入后的特征表达,如果与某一颜色相关的每个 \(y\) 的目的网络表达都接近其对应的⭐,那么表达迁移性就很高。当表达转移性较低时,针对同一目标图像生成的目达表达对抗样本的是不相似的,因此在图中不会出现分组的情况。
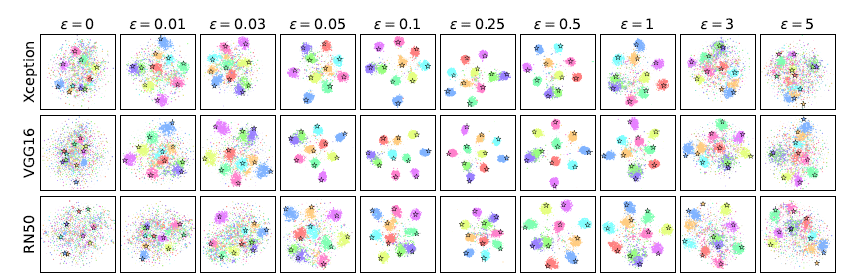

图 3:使用特定 "鲁棒性 "的白盒 ResNet50 模型生成的目标表达的对抗样本在目标模型表达的t-SNE图。底部的10张图片是来自ImageNet 的图片,我们将其作为表达目标,如文中所述。(最好以彩色和放大的方式观看)。
另外一种是采用平均余弦相似度度量(\(x\),\(y\))在目标模型表达的相似度(表 2),平均余弦相似度越高,表示从源网络到对应的目标网络的表达迁移程度越高。
表 2:平均余弦相似度,每一个值都是9900个 (\(x\),\(y\)) 目标表达相似度的平均
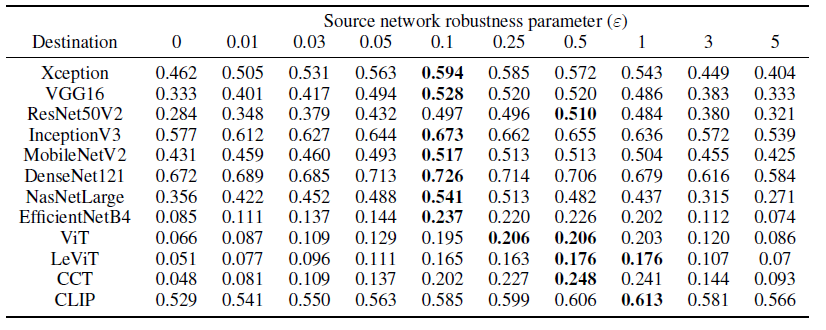
非鲁棒的模型生成的目标对抗样本,即使对抗分类结果成功迁移,但对于大部分目标模型(\(\epsilon = 0\)),特征表达没有充分迁移。这意味着 非鲁棒网络的特征可能不会彼此严重重叠。表2和图3观察到用非鲁棒网络生成的对抗样本对 DenseNet121 有一定程度的表达迁移性,这可能解释了图1中观察到的对 DenseNet121 的高度类转迁移性。
但从稍微鲁棒的 ResNet50 分类器到 CLIP 的表示转移性是很高的,原因可能是 CLIP 不是在传统的分类问题上训练出来的,而是被训练来对图像和相应的文本描述进行类似的编码有关。高表达迁移性说明了略微鲁棒的网络的特征与每个被测试的(非鲁棒的)目标网络的特征有很大的重叠。
当网络以大的 "\(\epsilon\) "进行对抗性训练时,它们学到的特征与非鲁棒网络的特征重叠的程度随着 "$\("的增加而减少。我们推测,某些非鲁棒的特征会被具有足够大的 "\)$ "的鲁棒神经网络所忽略,因此当鲁棒性增加到一定程度时,非鲁棒网络的许多特征会被忽略,表达的可迁移性会下降。
总结与改进
本文主要研究了略微鲁棒的模型可以促进目标表达对抗样本的迁移,可能的原因是略微鲁棒的模型表达和目标模型表达有很大的重叠,当源模型过于鲁棒时,会忽略对于目标模型分类重要的非鲁棒特征,造成攻击迁移率下降。这两条规律对 CNN 和 transformer 都适用。
参考文献
[1] Y. Liu, X. Chen, C. Liu, and D. Song. Delving into transferable adversarial examples and black-box attacks. arXiv preprint arXiv:1611.02770, 2016.
[2] J. M. Springer, M. Mitchell, and G. T. Kenyon. Adversarial perturbations are not so weird: Entanglement of robust and non-robust features in neural network classifiers. arXiv preprint arXiv:2102.05110, 2021.