Towards Transferable Adversarial Attacks on Vision Transformers

目前是关于transformer迁移攻击sota，发表在AAAI 2022，代码链接：https://github.com/zhipeng-wei/PNA-PatchOut

对于transformer的攻击要同时考虑patch和self-attention，本文提出 Pay No Attention (PNA) 攻击和 PatchOut 攻击，在反向传播时跳过注意力可以提高迁移性，同时攻击最优的一部分patch比攻击所有的patch效果好。实验证明所提方法可以提高ViTs之间的迁移和ViTs到CNNs的迁移。

PNA攻击固定attention前向计算数值，在反向传播时跳过这一部分梯度的计算，这阻止了不同patch之间的交互，图像不同区域之间的交互强度和迁移性是负相关的[1]。

PatchOut 攻击在每一次迭代随机选择一部分patch攻击，有点像drop-out缓解过拟合，这和随机森林随机选择特征和DIM攻击相似。

本文主要贡献点

PAN攻击不经过对attention的反向传播构造对抗样本。
研究扰动随机patch子集可以提高迁移性，提出PatchOut 方法在每轮迭代时使用不同的patch作为输入。
4个不同白盒ViTs，8个黑盒ViTs，4个黑盒CNNs，3个鲁棒训练CNNs进行实验，两种攻击方法有效并且可以和其他方法结合。

对于第一二点贡献进行了两个toy experiments，ViT-B/16白盒模型的BIM攻击（$L_{\infty}$范数下，迭代10次，$\epsilon = 16$），PNA攻击，将12个Self-attention Block分为3组，反向传播时就有八条路线，攻击成功率见下图

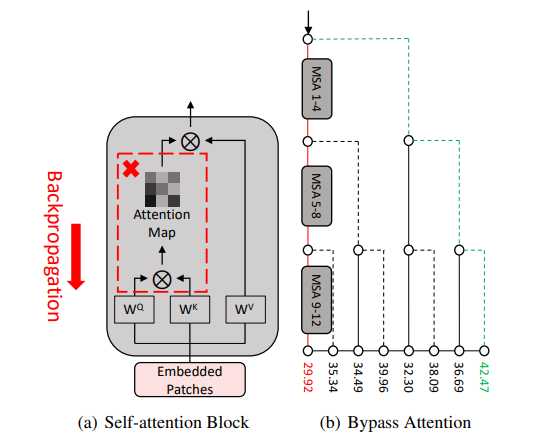
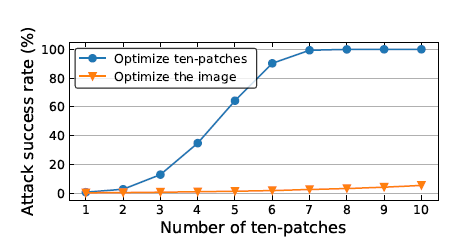
PatchOut 攻击随机选取10个patchs作为一种输入模式，记为“ten-patch”，进行多次“ten-patch”攻击成功率高

方法

Pay No Attention (PNA)

给定一个patch embedding $Z\in \mathbb{R}^{N\times D}$，query，key，和value 权重$W^{Q}$，$W^{K}$，$W^{V}$$\in$ $\mathbb{R}^{D\times D_h}$，attention计算如下 \[ A=\operatorname{softmax}\left(Z W^{Q}\left(Z W^{K}\right)^{T} / \sqrt{D_{h}}\right) \] $A\in\mathbb{R}^{N\times N}$表示注意力权重，一个head的输出定义如下 \[ Z^{\prime}=A\left(Z W^{V}\right) \] 输出$Z^{\prime}$对于输入$Z$的梯度如下 \[ \frac{\partial Z^{\prime}}{\partial Z}=(\mathbb{I} \bigotimes A) \frac{\partial\left(Z W^{V}\right)}{\partial Z}+\left(\left(Z W^{V}\right)^{T} \bigotimes \mathbb{I}\right) \frac{\partial A}{\partial Z} \] PNA方法忽视注意力部分的梯度，$\frac{\partial A}{\partial Z}=0$，这相当于将attention weights固定为一个常数。最终梯度计算如下 \[ \frac{\partial Z^{\prime}}{\partial Z} \approx(\mathbb{I} \bigotimes A) \frac{\partial\left(Z W^{V}\right)}{\partial Z}=(\mathbb{I} \bigotimes A)\left(\left(W^{V}\right)^{T} \bigotimes \mathbb{I}\right) \] $\bigotimes$表示克罗内克积，PNA迫使扰动只通过使用特征表征来利用网络，而不是通过利用注意力的高度模型特定属性。这导致了具有高迁移性的对抗样本。跳过注意力也允许梯度关注每个patch，而不是依赖patch之间的复杂相互作用。

PatchOut Attack

DIM攻击表明输入多样性有利于对抗向本迁移，PatchOut Attack每次迭代随机选择patch子集攻击。

用$T$控制每一轮使用的patch数量，$x_s=\{x_s^{1},...,x_s^{t},...,x_s^{T}\}$表示被选择的patch，攻击的mask $M\in {0,1}^{H\times W\times C}$ 定义如下 \[ M_{p}^{i}= \begin{cases}1, & \text { if } x_{p}^{i} \text { in } x_{s} \\ 0, & \text { otherwise }\end{cases} \] $M_{p}^{i} \in\{0,1\}^{P \times P \times C}$是$x_p ^{i}$在图像中区域，整个攻击的优化目标 \[ \underset{\delta}{\arg \max } J(f(x+M \odot \delta), y)+\lambda\|\delta\|_{2}$, s.t. $\|\delta\|_{\infty}<\epsilon \] $\odot$是element-wise乘法，第二项鼓励扰动有一个较大的$l_2$范数，两种攻击的伪代码如下

实验结果

在CNNS上的效果

数据集：ImageNet val中1000张不同类所有模型正确分类图像，白盒模型 ViT-B/16，PiT-B，CaiT-S-24，Visformer-S，图中每个数据都是四种替代模型迁移攻击成功率的平均。

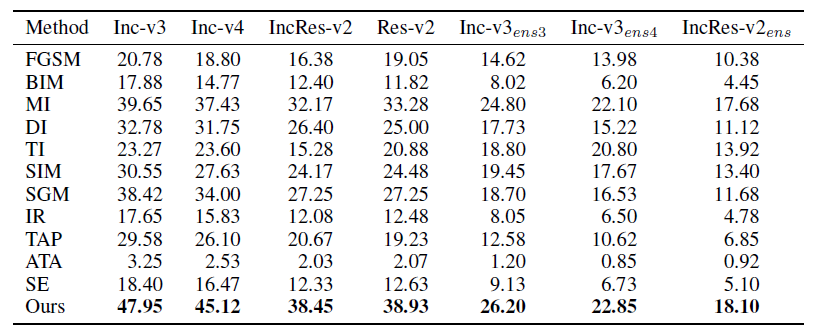
本文方法和之前方法的结合，白盒模型ViT-B/16，表中是平均迁移攻击成功率，8个ViTs：ViT-B/16，DeiT-B，TNT-S，LeViT-256，PiT-B ，CaiT-S-24，ConViT-B 和 Visformer-S，4个CNNs：Inception v3 (Inc-v3)，Inception v4 (Incv4)，Inception ResNet v2 (IncRes-v2)，和 ResNet v2-152 (Res-v2)。

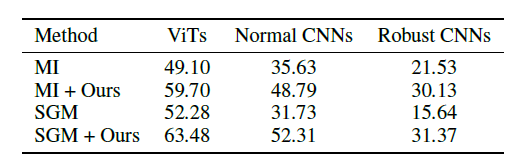
消融实验

白盒模型 ViT-B/16，数据 2000张随机采样图像，平均迁移攻击成功率

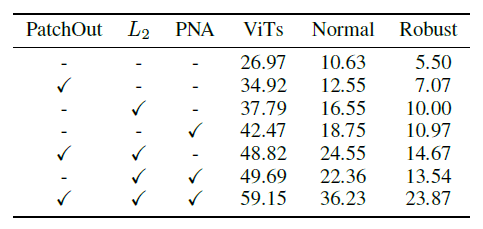
三部分都有效，一起使用效果最佳

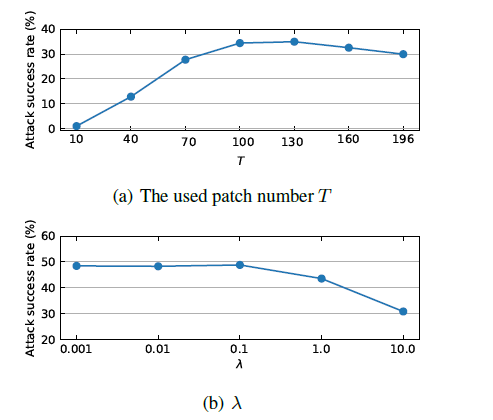
超参数影响，ViTs 平均攻击成功率 $T=N$ PatchOut 退化成 BIM，

[1] Wang, X.; Ren, J.; Lin, S.; Zhu, X.;Wang, Y.; and Zhang, Q.2020. A unified approach to interpreting and boosting adversarial transferability. arXiv preprint arXiv:2010.04055.