Yet Another Intermediate-Level Attack(ECCV 2020)
代码:https://github.com/qizhangli/ila-plus-plus
本篇也是利用网络中间层进行攻击,是[1]的延续。本文的主要思想是建立一个由中间层特征到对抗损失的映射\(W\),生成具有最大预期对抗损失的像素级扰动。在本文中定的对抗扰动是交叉熵损失。作者认为映射\(W\)包含了baseline攻击方法的每一步的信息,比单独使用最后一次迭代的结果更具有引导作用。
主要方法
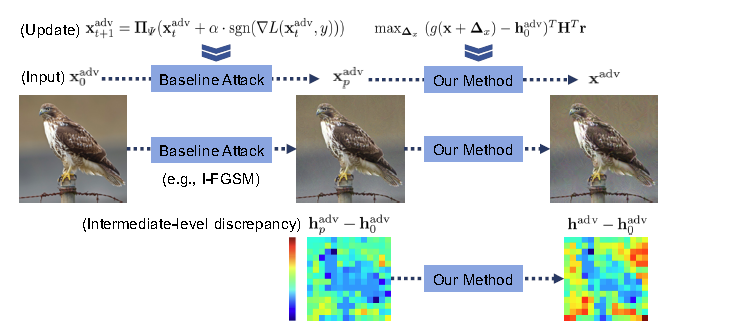
由上面的动机可知本文的关键是如何利用baseline方法每一步的信息构建映射\(W\)。假设中间层特征用\(h_t^{adv}=g(x_t^{adv})\)表示。baseline每一步生成的对抗样本\(x_0^{adv},...x_t^{adv},...x_{p}^{adv}\),可以得到一系列的中间层差异和对抗损失\(\{(h_t^{adv}-h_0^{adv},l_t)\}\),建立一个映射\(W\)直接由中间层差异预测对抗损失,\(W\)可以看成下面的优化问题: \[ \min _{\mathbf{w}} \sum_{t=0}^p\left(\mathbf{w}^T\left(\mathbf{h}_t^{adv}-\mathbf{h}_0^{adv}\right)-l_t\right)^2+\lambda\|\mathbf{w}\|^2 \tag{1} \] \(W\in \mathbb{R}^m,H\in \mathbb{R}^{(p+1)\times m},r \in \mathbb{R}^{p+1}\),上面优化问题写成向量/矩阵形式: \[ \min _{\mathbf{w}} \|\mathbf{r}-\mathbf{HW}\|^2+\lambda\|\mathbf{W}\|^2 \] 上述问题有闭式解\(\mathbf{W^{\star}}=(\mathbf{H^{\top}H+\lambda I_m})^{-1}\mathbf{H^{\top}r}\),整个优化过程: \[ \max _{\Delta_w}\left(g\left(\mathbf{x}+\Delta_x\right)-\mathbf{h}_0^{\text {adv }}\right)^{\top} \mathbf{w}^{\star}, \quad s.t. \left(\mathbf{x}+\boldsymbol{\Delta}_x\right) \in \Psi \] \((\mathbf{H^{\top}H+\lambda I_m}) \in \mathbb{R}^{m\times m}\)\(p\),计算它的逆矩阵困难,\(m\)一般都远大于\(p\),使用Woodbury等式变换 \[ \begin{aligned} \mathrm{H}^{\top} \mathrm{H}+\lambda \mathrm{I}_m & =\frac{1}{\lambda} I-\frac{1}{\lambda^2} \mathrm{H}^{\top}\left(\frac{1}{\lambda} \mathrm{HH}^{\top}+\mathrm{I}_p\right)^{-1} \mathrm{H} \\ & =\frac{1}{\lambda} I-\frac{1}{\lambda} \mathrm{H}^{\top}\left(\mathrm{HH}^{\top}+\lambda \mathrm{I}_p\right)^{-1} \mathrm{H} \end{aligned} \] 现在只需要计算\(\mathbf{HH^{\top}+\lambda I_p}\)的逆即可,当正则化参数\(\lambda\)非常大时,\(\mathrm{H}^{\top}\left(\mathrm{HH}^{\top}+\lambda \mathrm{I}_p\right)^{-1} \mathrm{H}\approx 0\),这种情况下优化问题近似于$ _{_w}(g(+_x)-_0^{a dv} )^{} ^{} \(,如果只考虑\)x_p{adv}\(和干净样本的差异或者baseline时单步攻击,优化问题退化为ILA。\){} $也可以看作是一系列投影方向的线性组合,充分利用baseline的时序信息提高迁移能力。
考虑到不同迭代步数是中间层差异数值差异较大,在求解公式1之前对中间层差异进行归一化,用\(\tilde{H}\)代替\(H\),\(\tilde{H}\)第\(t\)行表示为\((h_t^{adv}-h_t^{0})/\|h_t^{adv}-h_t^{0}\|\)。
总结与改进
充分利用baseline每步迭代信息值得借鉴。
参考文献
[1] Enhancing adversarial example transferability with an intermediate level attack.